平衡二叉樹也稱為高度平衡樹。當左子樹和右子樹的高度之差不大于 m 時，它被定義為二叉樹，其中 m 通常等于 1。樹的高度是兩棵樹之間最長路徑上的邊數根節點和葉節點。

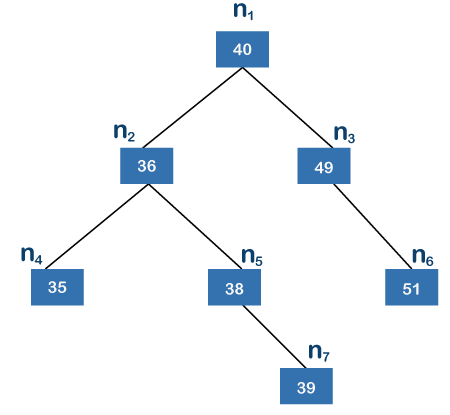
上面的樹是二叉搜索樹。二叉搜索樹是一棵樹，其中左側每個節點的值都低于其父節點，而右側節點的值高于其父節點。在上面的樹中，n1 是根節點，n4、n6、n7 是葉子節點。n7 節點是離根節點最遠的節點。n4 和 n6 包含 2 條邊，根節點和 n7 節點之間存在 3 條邊。由于 n7 離根節點最遠;因此，上述樹的高度為 3。

現在我們將看看上面的樹是否平衡。左子樹包含節點 n2、n4、n5 和 n7，而右子樹包含節點 n3 和 n6。左子樹有兩個葉子節點，即n4 和n7。節點 n2 和 n4 之間只有一條邊，節點 n7 和 n2 之間只有兩條邊;因此，節點 n7 離根節點最遠。左子樹的高度為2。右子樹只包含一個葉子節點，即n6，并且只有一條邊;因此，右子樹的高度為 1。左子樹和右子樹的高度之差為 1。由于我們得到的值為 1，所以我們可以說上面的樹是高度平衡的樹。這個計算高度差的過程應該針對每個節點(如 n2、n3、n4、n5、n6 和 n7)執行。

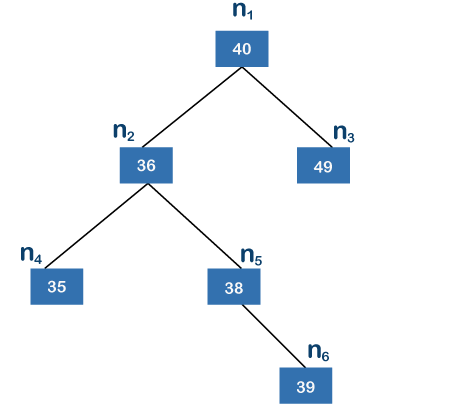
當我們處理每個節點時，二叉樹在上面的樹中，n6、n4 和 n3 是葉子節點，其中 n6 是離根節點最遠的節點。根節點和葉子節點之間存在三條邊;因此，上述樹的高度為 3。當我們將 n1 視為根節點時，左子樹包含節點 n2、n4、n5 和 n6，而子樹包含節點 n3。在左子樹中，n2 是根節點，n4 和 n6 是葉節點。在n4和n6個節點中，n6是離其根節點最遠的節點，n6有兩條邊;因此，左子樹的高度為 2。右子樹的左右兩側確實有任何子樹;因此，右子樹的高度為0。由于左子樹的高度為2，右子樹的高度為0，所以左子樹和右子樹的高度差為2。根據定義，左子樹和右子樹的高度之差一定不能大于1。此時差為2，大于1;因此，上述二叉樹是不平衡二叉搜索樹。

為什么我們需要平衡二叉樹?

讓我們通過一個例子來了解平衡二叉樹的必要性。

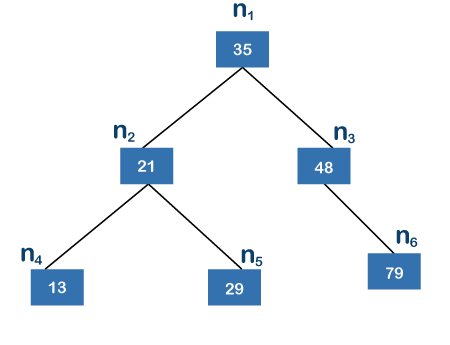
上面的樹是二叉搜索樹，因為所有左子樹節點都小于其父節點，所有右子樹節點都大于其父節點。假設我們想在上面的樹中找到值 79。首先，我們將節點 n1 的值與 79 進行比較;由于 79 的值不等于 35 而大于 35 所以我們移動到節點 n3，即 48。由于值 79 不等于 48 并且 79 大于 48，所以我們向右移動48 的子節點。節點 48 的右子節點的值為 79，等于要搜索的值。搜索元素 79 所需的跳數為 2，搜索任何元素所需的最大跳數為 2。搜索元素的平均情況為 O(logn)。

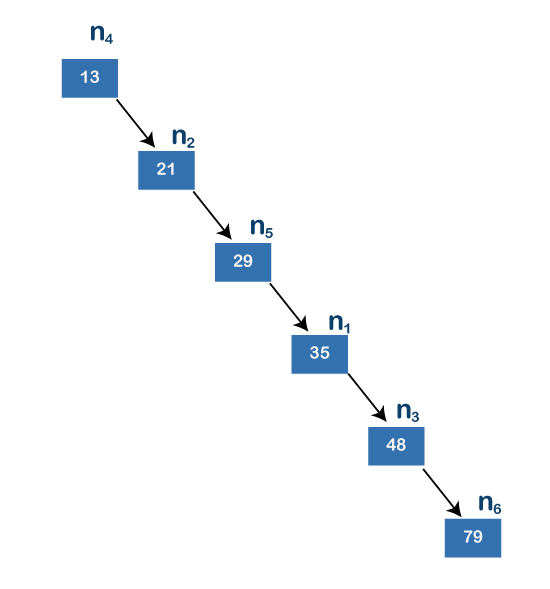
上面的樹也是二叉搜索樹，因為所有左子樹節點都小于其父節點，所有右子樹節點都大于其父節點。假設我們要在上面的樹中找到值 79。首先，我們將值 79 與節點 n4 即 13 進行比較。由于值 79 大于 13，所以我們移動到節點 13 的右子節點，即 n2 (21)。節點 n2 的值為 21 小于 79，所以我們再次移動到節點 21 的右側。節點 21 的右孩子的值為 29。由于值 79 大于 29，所以我們向右移動節點29的子節點。節點29的右孩子的值為35，小于79所以我們移動到節點35的右孩子，即48。值79大于48，所以我們移動到右孩子節點 48。48 的右子節點的值為 79，等于要搜索的值。在這種情況下，搜索一個元素所需的跳數是 5。在這種情況下，最壞的情況是 O(n)。

如果節點數增加，則樹形圖 1 中使用的公式比樹形圖 2 中使用的公式更有效。假設上述兩棵樹中可用的節點數均為 100,000。在樹形圖中搜索任何元素所需的時間為 100,000 µs，而在樹形圖中搜索元素所需的時間為 log(100,000)，即 16.6 µs。我們可以觀察到上述兩棵樹之間的巨大時間差異。因此，我們得出結論，平衡二叉樹比線性樹數據結構提供更快的搜索。

以上就是關于“平衡二叉查找樹”的介紹，想學習更多的神奇的算法和數據結構，可以關注一下動力節點的數據結構和算法教程，里面的課程內容細致全面，通俗易懂，是你的不二選擇。