更新時間:2022-09-27 10:12:05 來源:動力節點 瀏覽1434次
完全二叉樹查找效率及深度是什么?動力節點小編來告訴大家。二叉搜索樹也可稱為二叉查找樹(詳解二叉查找樹操作),我們在樹, 二叉樹, 二叉搜索樹中提到,一個有n個節點的二叉樹,它的最小深度為log(n),最大深度為n。比如下面兩個二叉樹:
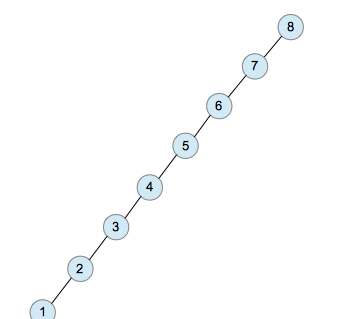
深度為n的二叉樹
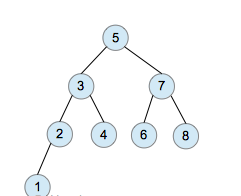
這兩個二叉樹同時也是二叉搜索樹(參考樹, 二叉樹, 二叉搜索樹)。注意,log以2為基底。log(n)是指深度的量級。根據我們對深度的定義,精確的最小深度為floor(log(n)+1)。
我們將處于同一深度的節點歸為一層。如果除最后一層外的其他層都被節點填滿時,二叉樹有最小深度log(n)。
二叉搜索樹的深度越小,那么搜索所需要的運算時間越小。一個深度為log(n)的二叉搜索樹,搜索算法的時間復雜度也是log(n)。然而,我們在二叉搜索樹中已經實現的插入和刪除操作并不能讓保持log(n)的深度。如果我們按照8,7,6,5,4,3,2,1的順序插入節點,那么就是一個深度為n的二叉樹。那么,搜索算法的時間復雜度為n。
n和log(n)的時間復雜度意味著什么呢?時間復雜度代表了完成算法所需要的運算次數。時間復雜度越小,算法的速度越快。
可以看到,隨著元素的增加,log(n)的時間復雜度的增長要遠小于n。所以,我們自然希望二叉搜索樹能盡可能保持log(n)的深度。在上面深度為n的例子中,我們發現,每個節點只有左節點被填滿。樹的每一層都有很多空位。能不能盡可能減少每一層的空位呢? (相應的,減少樹的深度)
一種想法是先填滿一層,再去填充下一層,這樣就是一個完全二叉樹(complete binary tree)。這樣的二叉樹實現插入算法會比較復雜。
以上就是關于“完全二叉樹查找效率及深度”的介紹,大家如果對此比較感興趣,想了解更多相關知識,不妨來關注一下動力節點的Java在線學習,里面的課程內容從入門到精通,細致全面,適合沒有基礎的小伙伴學習,希望對大家能夠有所幫助。
 Java實驗班
Java實驗班
0基礎 0學費 15天面授
 Java就業班
Java就業班
有基礎 直達就業
 Java夜校直播班
Java夜校直播班
業余時間 高薪轉行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構師班
Java架構師班
工作3~5年,晉升架構
提交申請后,顧問老師會電話與您溝通安排學習