貪心算法，又名貪婪算法，顧名思義，是指在對問題求解時(shí)，總是作出在當(dāng)前看來最好的選擇。也就是說貪心算法并不從整體最優(yōu)考慮，它所作出的選擇只是在某種意義上的局部最優(yōu)選擇。

貪心算法不是對所有問題都能得到整體最優(yōu)解，關(guān)鍵是貪心策略的選擇，選擇的貪心策略必須具備無后效性，即某個(gè)狀態(tài)以前的過程不會(huì)影響以后的狀態(tài)，只與當(dāng)前狀態(tài)有關(guān)。雖然貪心算法不能對所有問題都得到整體最優(yōu)解，但對許多問題它能產(chǎn)生整體最優(yōu)解。如單源最短路經(jīng)問題，最小生成樹問題，背包最大價(jià)值問題等。在一些情況下，即使貪心算法不能得到整體最優(yōu)解，其最終結(jié)果卻是最優(yōu)解的很好近似。

這里我們采用更容易理解的背包最大價(jià)值問題：

有一個(gè)背包，最多能承載重量為 C=150的物品，現(xiàn)在有7個(gè)物品（物品不能分割成任意大小），編號為 1~7，重量分別是 wi=[35,30,60,50,40,10,25]，價(jià)值分別是 pi=[10,40,30,50,35,40,30]，現(xiàn)在從這 7 個(gè)物品中選擇一個(gè)或多個(gè)裝入背包，要求在物品總重量不超過 C 的前提下，所裝入的物品總價(jià)值最高。這里需要明確的幾個(gè)點(diǎn)：1.每個(gè)物品都有重量和價(jià)值兩個(gè)屬性；2.每個(gè)物品分被選中和不被選中兩個(gè)狀態(tài)（后面還有個(gè)問題，待討論）；3.可選物品列表已知，背包總的承重量一定。所以，構(gòu)建描述每個(gè)物品的數(shù)據(jù)體結(jié)構(gòu) OBJECT和背包問題定義為：//typedef是類型定義的意思

//定義待選物體的結(jié)構(gòu)體類型
typedef struct tagObject
{
????int weight;
????int price;
????int status;
}OBJECT;

//定義背包問題
typedef struct tagKnapsackProblem
{
????vector<OBJECT>objs;
????int totalC;
}KNAPSACK_PROBLEM;

如下,實(shí)例化objectsOBJECT objects[] = { { 35,10,0 },{ 30,40,0 },{ 60,30,0 },{ 50,50,0 },

                    { 40,35,0 },{ 10,40,0 },{ 25,30,0 } };

那么，我們思考一下，如何選，才使得裝進(jìn)背包的價(jià)值最大呢？

策略1：價(jià)值主導(dǎo)選擇，每次都選價(jià)值最高的物品放進(jìn)背包；

策略2：重量主導(dǎo)選擇，每次都選擇重量最輕的物品放進(jìn)背包；

策略3：價(jià)值密度主導(dǎo)選擇，每次選擇都選價(jià)值/重量最高的物品放進(jìn)背包。

策略1：價(jià)值主導(dǎo)選擇

每次都選價(jià)值最高的物品放進(jìn)背包根據(jù)這個(gè)策略最終選擇裝入背包的物品編號依次是 4、2、6、5，此時(shí)包中物品總重量是 130，總價(jià)值是 165。//遍歷沒有被選的objs,并且選擇price最大的物品,返回被選物品的編號

int Choosefunc1(std::vector<OBJECT>& objs, int c)
{
????int index = -1; ?//-1表示背包容量已滿
????int max_price = 0;
????//在objs[i].status == 0的物品里，遍歷挑選objs[i].price最大的物品
????for (int i = 0; i < static_cast<int>(objs.size()); i++)
????{
????????if ((objs[i].status == 0) && (objs[i].price > max_price ))//objs沒有被選,并且price> max_price
????????{
????????????max_price ?= objs[i].price;
????????????index = i;
????????}
????}
????return index;
}

策略2：重量主導(dǎo)選擇

每次都選擇重量最輕(小)的物品放進(jìn)背包根據(jù)這個(gè)策略最終選擇裝入背包的物品編號依次是 6、7、2、1、5，此時(shí)包中物品總重量是 140，總價(jià)值是 155。int Choosefunc2(std::vector<OBJECT>& objs, int c)

{
????int index = -1;
????int min_weight= 10000;
????for (int i = 0; i < static_cast<int>(objs.size()); i++)
????{
????????if ((objs[i].status == 0) && (objs[i].weight < min_weight))
????????{
????????????min_weight= objs[i].weight;
????????????index = i;
????????}
????}
????return index;
}

策略3：價(jià)值密度主導(dǎo)選擇

每次選擇都選價(jià)值/重量最高(大)的物品放進(jìn)背包物品的價(jià)值密度 si 定義為 pi/wi，這 7 件物品的價(jià)值密度分別為 si=[0.286,1.333,0.5,1.0,0.875,4.0,1.2]。根據(jù)這個(gè)策略最終選擇裝入背包的物品編號依次是 6、2、7、4、1，此時(shí)包中物品的總重量是 150，總價(jià)值是 170。int Choosefunc3(std::vector<OBJECT>& objs, int c)

{
????int index = -1;
????double max_s = 0.0;
????for (int i = 0; i < static_cast<int>(objs.size()); i++)
????{
????????if (objs[i].status == 0)
????????{
????????????double si = objs[i].price;
????????????si = si / objs[i].weight;
????????????if (si > max_s)
????????????{
????????????????max_s = si;
????????????????index = i;
????????????}
????????}
????}
????return index;
}

回過頭來，我們再來根據(jù)貪心算法的定義來對這個(gè)問題進(jìn)行貪心算法GreedyAlgo：

void GreedyAlgo
(KNAPSACK_PROBLEM *problem, SELECT_POLICY spFunc)
{
????int idx;
????int sum_weight_current = 0;
????//先選
????while ((idx = spFunc(problem->objs, problem->totalC- sum_weight_current)) != -1)
????{ ??//再檢查，是否能裝進(jìn)去
????????if ((sum_weight_current + problem->objs[idx].weight) <= problem->totalC)
????????{
????????????problem->objs[idx].status = 1;//如果背包沒有裝滿，還可以再裝,標(biāo)記下裝進(jìn)去的物品狀態(tài)為1
????????????sum_weight_current += problem->objs[idx].weight;//把這個(gè)idx的物體的重量裝進(jìn)去，計(jì)算當(dāng)前的重量
????????}
????????else
????????{
????????????//不能選這個(gè)物品了，做個(gè)標(biāo)記2后重新選剩下的
????????????problem->objs[idx].status = 2;
????????}
????}
????PrintResult(problem->objs);//輸出函數(shù)的定義，查看源代碼
}

主函數(shù)部分OBJECT objects[] = { { 35,10,0 },{ 30,40,0 },{ 60,30,0 },{ 50,50,0 },                

????{ 40,35,0 },{ 10,40,0 },{ 25,30,0 } };
int main()
{
????KNAPSACK_PROBLEM problem;
????problem.objs.assign(objects, objects + 7);//assign賦值，std::vector::assign
????problem.totalC = 150;
????cout << "Start to find the best way ,NOW" << endl;
????GreedyAlgo(&problem, Choosefunc3);
????system("pause");
????return 0;
}

策略3的輸出結(jié)果：

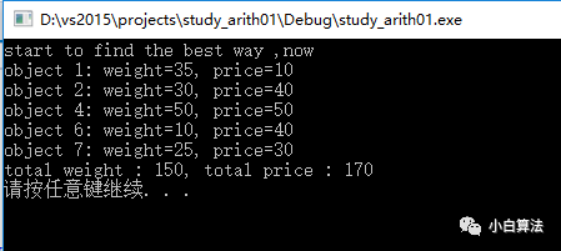
通過上面的背包價(jià)值最大問題，我們不難看出：貪心算法總體來說簡單，高效，省去了為了找最優(yōu)解可能需要窮舉操作，通常作為其它算法的輔助算法來使用；但貪心算法不從總體上考慮其它可能情況，每次選取局部最優(yōu)解，不再進(jìn)行回溯處理，所以很少情況下得到最優(yōu)解。貪心算法只是眾多優(yōu)秀算法中的一員，想要了解更多神奇的算法可以觀看本站的數(shù)據(jù)結(jié)構(gòu)和算法教程，學(xué)習(xí)新的算法知識。